3. Finite element model of an electrodynamic loudspeaker

In this paper, the equations governing the magnetic, mechanical and acoustic field quantities are solved using a Finite-Element-Method (FEM). The theory of the underlying finite element scheme has already been reported in [2] and will not be repeated here. Meanwhile, this scheme has been updated with respect to the modeling of a voltage loaded moving coil to allow the efficient and precise simulation of electrodynamic loudspeakers [10]. It should be noted, however, that the computer modeling presented in this work is currently limited by the assumption, that the loudspeaker has to be operated within the so-called jump-out excursion [9], where the voice coil begins to leave the magnet gap. In this case the length of the voice coil wire immersed in the gap field is constant and, therefore, re-meshing of the simulation area is not required [10]. Furthermore, nonlinear effects in the mechanical behavior of the loudspeaker have been ignored.

In finite element methods, the region under consideration (region of the electromechanical device with air surroundings) is subdivided into small discrete elements, the so-called finite elements. The finite element discretization of the moving coil driver (see Figure 1) is shown in Figure 2. Due to rotational symmetry, a two-dimensional finite element model based on axisymmetric elements suffices.

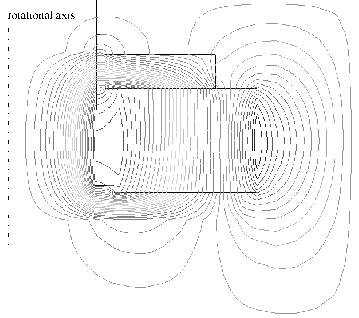
The voice coil and the lower part of the aluminum former are discretized by so-called magnetomechanical finite elements, which solve the equations governing the magnetic and mechanical field quantities (see equation (4) and (6)) and take account of the full coupling between these fields (see section 2.4). Due to the concentration of the magnetic flux within the magnet assembly, as shown in Figure 3, the magnet structure and only a small ambient region have to be discretized by magnetic finite elements. Finally, the surround, suspension, dust cap, cone diaphragm and the upper part of the aluminum former are modeled by pure mechanical finite elements (elements without magnetic energy).

  

Abbildung 2: 2D finite element model of an electrodynamic loudspeaker

  

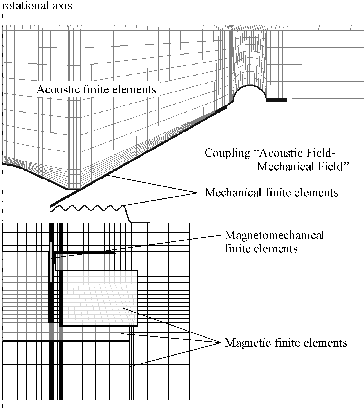Abbildung 3: Computed magnetic field distribution generated by the permanent magnet.

Additionally, the following aspects have to be considered for the precise computer simulation of electrodynamic loudspeakers:

• Since in most measurements the loudspeakers are mounted in practically infinite rigid baffles, only the fluid in front of the loudspeaker is modeled (see Figure 2). Therewith, the rigid baffle is taken into account and the size of the finite element mesh is nearly halved. However, now the material properties of the fluid, as used in the simulation, require special considerations.

  Generally, the influences of the surrounding air are mass-loading effects and damping due to the sound emission. In this case, where the frequency range is about 10 Hz - 10 kHz, the damping can be neglected. On the other hand, due to the considerable influence of the mass-loading on the fundamental resonance ($-8\%$ compared with no air loading) and on the sound pressure, the additional air loading of the lower fluid region has to be also taken into account. Here, the lower fluid region was not modeled to save computer capacity. Therefore, the mass-loading has to be increased by doubling the density and bulk modulus of the modeled upper air region.

• The fluid region is surrounded by acoustic infinite elements, which have to be located in the far field of the moving coil driver in order to work correctly.
• In all simulations, the standard formulation for the finite element solution of structural mechanics and solids, which is the displacement-based method, was used. Since in this formulation, in which only the displacements are applied as unknown variables [3], so-called locking phenomena may occur, first order finite elements, i.e. 4-node quadrilaterals or 3-node triangles, can not be used effectively in the simulations. The underlying theory of these effects is reported in the literature [3]. In the simulation of the electrodynamic loudspeaker two locking phenomena can be observed: the so-called shear and the membrane locking. The first one is due to an excessive element distortion, i.e. low thickness/width-ratios, and may occur mainly in the cone diaphragm. The second results from high bending moments in combination with curved elements and is observed in the suspension and the surround. These locking effects result in a strong artifical stiffening and a corresponding frequency shift can be observed. In order to obtain reliable results, higher order elements have been used throughout the simulations.
• First simulation results showed that the pole and top plate near the magnet gap as well as almost the whole back plate of the magnet assembly are saturated (see Figure 3). This effect results in a local low relative permeability and, furthermore, in a decreased inductance of the voice coil which dominates the electrical input impedance at higher frequencies.

For the design of electrodynamic loudspeakers, the frequency dependence of the axial sound pressure level and the electrical input impedance are the most important parameters. For the computation of these parameters, a dynamic analysis using a short pulse excitation signal for the voltage between the two supply terminals of the coil was performed. It should be noted that further input parameters are the geometry of the electrodynamic loudspeaker, the density, modulus of elasticity, Poisson's ratio and loss-factor for the mechanical materials and the electrical conductivity as well as magnetization curves (B/H-curves) for the magnetic parts. After the computation of the response signals (current in the conductors of the moving coil resp. sound pressure level in the surrounding air), the fourier transformations of output and input signal have to be divided. It is well known from the theory of fourier transformation that the number of frequency samples is proportionally to the number of time samples. Therefore, a large number of time steps have to be performed to achieve a good frequency resolution - e.g. about 10.000 time steps for a frequency range of 0 - 20 kHz.